CUDA Convolutional Sparse Coding¶
This example demonstrates the use of the interface to the CUDA CSC solver extension package, with a test for the availablity of a GPU that runs the Python version of the ConvBPDN solver if one is not available, or if the extension package is not installed.
from __future__ import print_function
from builtins import input
import pyfftw # See https://github.com/pyFFTW/pyFFTW/issues/40
import numpy as np
from sporco import util
from sporco import signal
from sporco import fft
from sporco import metric
from sporco import plot
plot.config_notebook_plotting()
from sporco import cuda
from sporco.admm import cbpdn
# If running in a notebook, try to use wurlitzer so that output from the CUDA
# code will be properly captured in the notebook.
sys_pipes = util.notebook_system_output()
Load example image.
img = util.ExampleImages().image('barbara.png', scaled=True, gray=True,
idxexp=np.s_[10:522, 100:612])
Highpass filter example image.
npd = 16
fltlmbd = 20
sl, sh = signal.tikhonov_filter(img, fltlmbd, npd)
Load dictionary.
D = util.convdicts()['G:12x12x36']
Set up admm.cbpdn.ConvBPDN options.
lmbda = 1e-2
opt = cbpdn.ConvBPDN.Options({'Verbose': True, 'MaxMainIter': 250,
'HighMemSolve': True, 'RelStopTol': 5e-3,
'AuxVarObj': False})
If GPU available, run CUDA ConvBPDN solver, otherwise run standard Python version.
if cuda.device_count() > 0:
print('%s GPU found: running CUDA solver' % cuda.device_name())
tm = util.Timer()
with sys_pipes(), util.ContextTimer(tm):
X = cuda.cbpdn(D, sh, lmbda, opt)
t = tm.elapsed()
else:
print('GPU not found: running Python solver')
c = cbpdn.ConvBPDN(D, sh, lmbda, opt)
X = c.solve().squeeze()
t = c.timer.elapsed('solve')
print('Solve time: %.2f s' % t)
GeForce RTX 2080 Ti GPU found: running CUDA solver
Itn Fnc DFid Regℓ1 r s ρ
----------------------------------------------------------------
0 6.26e+04 6.25e+04 1.02e+04 6.47e-01 7.54e-01 1.50e+00
1 6.36e+04 6.35e+04 8.59e+03 3.36e-01 5.78e-01 1.50e+00
2 7.68e+04 7.67e+04 1.04e+04 3.20e-01 3.53e-01 1.11e+00
3 7.73e+04 7.72e+04 8.21e+03 2.50e-01 2.95e-01 1.11e+00
4 7.40e+04 7.40e+04 7.18e+03 2.21e-01 1.95e-01 1.00e+00
5 7.55e+04 7.55e+04 6.99e+03 1.65e-01 1.48e-01 1.00e+00
6 7.99e+04 7.98e+04 6.64e+03 1.28e-01 1.33e-01 1.00e+00
7 8.40e+04 8.39e+04 6.30e+03 1.06e-01 1.11e-01 1.00e+00
8 8.48e+04 8.48e+04 6.08e+03 8.85e-02 9.98e-02 1.00e+00
9 8.45e+04 8.45e+04 5.76e+03 7.54e-02 8.71e-02 1.00e+00
10 8.47e+04 8.47e+04 5.54e+03 6.90e-02 7.52e-02 9.06e-01
11 8.64e+04 8.63e+04 5.46e+03 5.92e-02 6.68e-02 9.06e-01
12 8.81e+04 8.81e+04 5.38e+03 5.15e-02 6.08e-02 9.06e-01
13 8.95e+04 8.95e+04 5.32e+03 4.85e-02 5.57e-02 8.12e-01
14 9.04e+04 9.03e+04 5.29e+03 4.61e-02 4.95e-02 7.38e-01
15 9.12e+04 9.11e+04 5.21e+03 4.15e-02 4.47e-02 7.38e-01
16 9.22e+04 9.21e+04 5.13e+03 3.75e-02 4.16e-02 7.38e-01
17 9.33e+04 9.33e+04 5.06e+03 3.41e-02 3.87e-02 7.38e-01
18 9.44e+04 9.44e+04 5.00e+03 3.12e-02 3.62e-02 7.38e-01
19 9.54e+04 9.53e+04 4.96e+03 3.04e-02 3.41e-02 6.68e-01
20 9.62e+04 9.62e+04 4.93e+03 2.83e-02 3.17e-02 6.68e-01
21 9.70e+04 9.70e+04 4.90e+03 2.65e-02 2.95e-02 6.68e-01
22 9.78e+04 9.78e+04 4.86e+03 2.48e-02 2.79e-02 6.68e-01
23 9.86e+04 9.85e+04 4.83e+03 2.33e-02 2.65e-02 6.68e-01
24 9.94e+04 9.93e+04 4.80e+03 2.30e-02 2.52e-02 6.09e-01
25 1.00e+05 1.00e+05 4.79e+03 2.19e-02 2.36e-02 6.09e-01
26 1.01e+05 1.01e+05 4.78e+03 2.08e-02 2.23e-02 6.09e-01
27 1.01e+05 1.01e+05 4.76e+03 1.98e-02 2.12e-02 6.09e-01
28 1.02e+05 1.02e+05 4.74e+03 1.88e-02 2.03e-02 6.09e-01
29 1.02e+05 1.02e+05 4.71e+03 1.80e-02 1.95e-02 6.09e-01
30 1.03e+05 1.03e+05 4.69e+03 1.72e-02 1.87e-02 6.09e-01
31 1.03e+05 1.03e+05 4.67e+03 1.64e-02 1.80e-02 6.09e-01
32 1.04e+05 1.03e+05 4.66e+03 1.58e-02 1.73e-02 6.09e-01
33 1.04e+05 1.04e+05 4.64e+03 1.51e-02 1.67e-02 6.09e-01
34 1.04e+05 1.04e+05 4.63e+03 1.45e-02 1.61e-02 6.09e-01
35 1.04e+05 1.04e+05 4.61e+03 1.39e-02 1.55e-02 6.09e-01
36 1.05e+05 1.05e+05 4.60e+03 1.34e-02 1.50e-02 6.09e-01
37 1.05e+05 1.05e+05 4.59e+03 1.29e-02 1.45e-02 6.09e-01
38 1.05e+05 1.05e+05 4.58e+03 1.25e-02 1.40e-02 6.09e-01
39 1.06e+05 1.06e+05 4.57e+03 1.20e-02 1.35e-02 6.09e-01
40 1.06e+05 1.06e+05 4.55e+03 1.16e-02 1.31e-02 6.09e-01
41 1.06e+05 1.06e+05 4.54e+03 1.12e-02 1.27e-02 6.09e-01
42 1.06e+05 1.06e+05 4.53e+03 1.08e-02 1.23e-02 6.09e-01
43 1.06e+05 1.06e+05 4.52e+03 1.05e-02 1.19e-02 6.09e-01
44 1.07e+05 1.07e+05 4.51e+03 1.01e-02 1.15e-02 6.09e-01
45 1.07e+05 1.07e+05 4.51e+03 1.02e-02 1.11e-02 5.56e-01
46 1.07e+05 1.07e+05 4.50e+03 9.94e-03 1.07e-02 5.56e-01
47 1.07e+05 1.07e+05 4.50e+03 9.67e-03 1.03e-02 5.56e-01
48 1.08e+05 1.08e+05 4.49e+03 9.39e-03 9.88e-03 5.56e-01
49 1.08e+05 1.08e+05 4.49e+03 9.12e-03 9.56e-03 5.56e-01
50 1.08e+05 1.08e+05 4.48e+03 8.85e-03 9.28e-03 5.56e-01
51 1.08e+05 1.08e+05 4.47e+03 8.60e-03 9.01e-03 5.56e-01
52 1.08e+05 1.08e+05 4.47e+03 8.35e-03 8.75e-03 5.56e-01
53 1.08e+05 1.08e+05 4.46e+03 8.11e-03 8.51e-03 5.56e-01
54 1.09e+05 1.09e+05 4.46e+03 7.88e-03 8.29e-03 5.56e-01
55 1.09e+05 1.09e+05 4.45e+03 7.65e-03 8.07e-03 5.56e-01
56 1.09e+05 1.09e+05 4.44e+03 7.44e-03 7.87e-03 5.56e-01
57 1.09e+05 1.09e+05 4.44e+03 7.24e-03 7.67e-03 5.56e-01
58 1.09e+05 1.09e+05 4.43e+03 7.04e-03 7.48e-03 5.56e-01
59 1.09e+05 1.09e+05 4.42e+03 6.85e-03 7.28e-03 5.56e-01
60 1.09e+05 1.09e+05 4.42e+03 6.67e-03 7.09e-03 5.56e-01
61 1.09e+05 1.09e+05 4.42e+03 6.49e-03 6.91e-03 5.56e-01
62 1.10e+05 1.10e+05 4.41e+03 6.32e-03 6.73e-03 5.56e-01
63 1.10e+05 1.10e+05 4.41e+03 6.16e-03 6.57e-03 5.56e-01
64 1.10e+05 1.10e+05 4.40e+03 6.00e-03 6.40e-03 5.56e-01
65 1.10e+05 1.10e+05 4.40e+03 5.84e-03 6.24e-03 5.56e-01
66 1.10e+05 1.10e+05 4.39e+03 5.69e-03 6.09e-03 5.56e-01
67 1.10e+05 1.10e+05 4.39e+03 5.55e-03 5.94e-03 5.56e-01
68 1.10e+05 1.10e+05 4.38e+03 5.41e-03 5.80e-03 5.56e-01
69 1.10e+05 1.10e+05 4.38e+03 5.27e-03 5.66e-03 5.56e-01
70 1.10e+05 1.10e+05 4.38e+03 5.14e-03 5.53e-03 5.56e-01
71 1.10e+05 1.10e+05 4.37e+03 5.02e-03 5.40e-03 5.56e-01
72 1.11e+05 1.11e+05 4.37e+03 4.89e-03 5.27e-03 5.56e-01
73 1.11e+05 1.11e+05 4.37e+03 4.77e-03 5.14e-03 5.56e-01
74 1.11e+05 1.11e+05 4.36e+03 4.66e-03 5.02e-03 5.56e-01
75 1.11e+05 1.11e+05 4.36e+03 4.55e-03 4.90e-03 5.56e-01
----------------------------------------------------------------
Solve time: 1.04 s
Reconstruct the image from the sparse representation.
shr = np.sum(fft.fftconv(D, X, axes=(0, 1)), axis=2)
imgr = sl + shr
print("Reconstruction PSNR: %.2fdB\n" % metric.psnr(img, imgr))
Reconstruction PSNR: 44.12dB
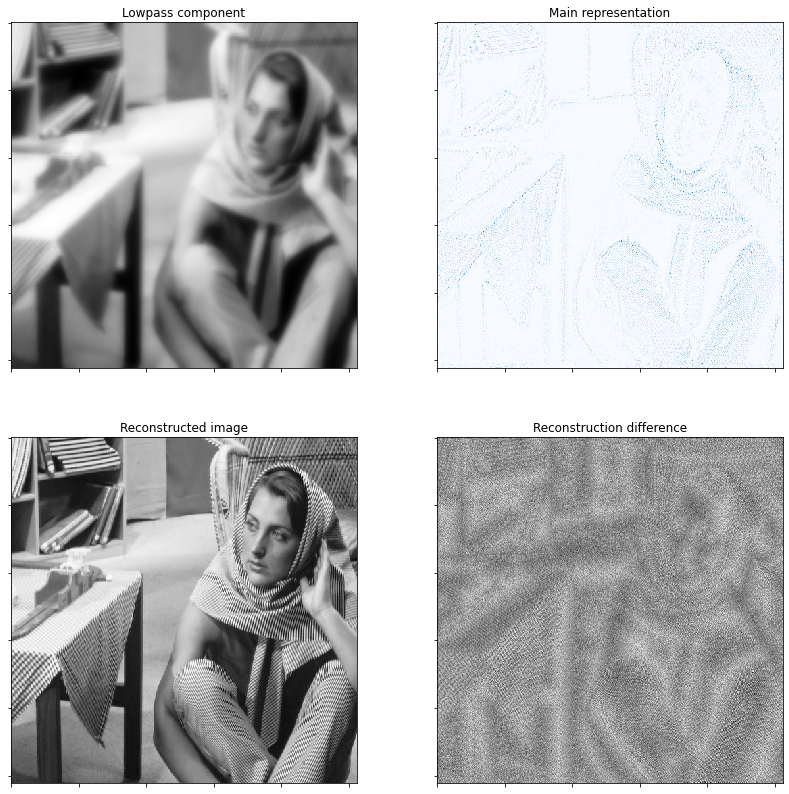
Display representation and reconstructed image.
fig = plot.figure(figsize=(14, 14))
plot.subplot(2, 2, 1)
plot.imview(sl, title='Lowpass component', fig=fig)
plot.subplot(2, 2, 2)
plot.imview(np.sum(abs(X), axis=2).squeeze(),
cmap=plot.cm.Blues, title='Main representation', fig=fig)
plot.subplot(2, 2, 3)
plot.imview(imgr, title='Reconstructed image', fig=fig)
plot.subplot(2, 2, 4)
plot.imview(imgr - img, fltscl=True, title='Reconstruction difference',
fig=fig)
fig.show()