ℓ1-Spline¶
This example demonstrates the use of class spline.SplineL1
for removing salt & pepper noise from a greyscale image using ℓ1-spline
fitting.
from __future__ import print_function
from builtins import input
import numpy as np
from sporco.admm import spline
from sporco import util
from sporco import signal
from sporco import metric
from sporco import plot
plot.config_notebook_plotting()
Load reference image.
img = util.ExampleImages().image('monarch.png', scaled=True,
idxexp=np.s_[:,160:672], gray=True)
Construct test image corrupted by 20% salt & pepper noise.
np.random.seed(12345)
imgn = signal.spnoise(img, 0.2)
Set regularization parameter and options for ℓ1-spline solver. The regularization parameter used here has been manually selected for good performance.
lmbda = 5.0
opt = spline.SplineL1.Options({'Verbose': True, 'gEvalY': False})
Create solver object and solve, returning the the denoised image
imgr.
b = spline.SplineL1(imgn, lmbda, opt)
imgr = b.solve()
Itn Fnc DFid Reg r s ρ
----------------------------------------------------------------
0 4.13e+04 3.23e+04 1.79e+03 2.22e-01 3.80e+00 1.01e+01
1 3.52e+04 3.35e+04 3.35e+02 1.17e-01 1.98e+00 1.01e+01
2 3.88e+04 3.68e+04 4.02e+02 1.36e-01 3.60e-01 2.45e+00
3 3.51e+04 3.35e+04 3.17e+02 1.06e-01 2.35e-01 1.51e+00
4 3.31e+04 3.15e+04 3.18e+02 8.13e-02 1.22e-01 1.01e+00
5 3.34e+04 3.18e+04 3.07e+02 6.81e-02 6.62e-02 8.27e-01
6 3.21e+04 3.05e+04 3.09e+02 5.03e-02 5.41e-02 8.27e-01
7 3.10e+04 2.94e+04 3.08e+02 3.74e-02 4.22e-02 8.27e-01
8 3.08e+04 2.92e+04 3.08e+02 2.98e-02 2.87e-02 8.27e-01
9 3.04e+04 2.89e+04 3.05e+02 2.34e-02 2.34e-02 8.27e-01
10 3.01e+04 2.85e+04 3.07e+02 1.88e-02 1.84e-02 8.27e-01
11 2.99e+04 2.84e+04 3.05e+02 1.58e-02 1.33e-02 8.27e-01
12 2.98e+04 2.83e+04 3.06e+02 1.34e-02 1.08e-02 8.27e-01
13 2.97e+04 2.82e+04 3.05e+02 1.15e-02 9.18e-03 9.22e-01
14 2.96e+04 2.81e+04 3.05e+02 1.02e-02 7.46e-03 1.03e+00
15 2.96e+04 2.81e+04 3.04e+02 9.16e-03 6.82e-03 1.21e+00
16 2.96e+04 2.80e+04 3.05e+02 8.40e-03 6.09e-03 1.40e+00
17 2.95e+04 2.80e+04 3.04e+02 7.74e-03 5.45e-03 1.64e+00
18 2.95e+04 2.80e+04 3.05e+02 7.15e-03 5.32e-03 1.95e+00
19 2.95e+04 2.80e+04 3.05e+02 6.58e-03 4.97e-03 2.27e+00
20 2.95e+04 2.79e+04 3.05e+02 6.06e-03 4.80e-03 2.61e+00
21 2.94e+04 2.79e+04 3.05e+02 5.55e-03 4.45e-03 2.93e+00
22 2.94e+04 2.79e+04 3.06e+02 5.08e-03 4.38e-03 3.27e+00
23 2.94e+04 2.79e+04 3.06e+02 4.65e-03 3.71e-03 3.27e+00
24 2.94e+04 2.78e+04 3.07e+02 4.26e-03 3.72e-03 3.66e+00
25 2.93e+04 2.78e+04 3.07e+02 3.90e-03 3.26e-03 3.66e+00
26 2.93e+04 2.78e+04 3.08e+02 3.59e-03 2.85e-03 3.66e+00
27 2.93e+04 2.78e+04 3.08e+02 3.29e-03 2.85e-03 4.11e+00
28 2.93e+04 2.78e+04 3.09e+02 3.02e-03 2.61e-03 4.11e+00
29 2.93e+04 2.78e+04 3.09e+02 2.78e-03 2.27e-03 4.11e+00
30 2.93e+04 2.77e+04 3.10e+02 2.56e-03 2.27e-03 4.54e+00
31 2.93e+04 2.77e+04 3.11e+02 2.35e-03 2.03e-03 4.54e+00
32 2.93e+04 2.77e+04 3.11e+02 2.16e-03 1.81e-03 4.54e+00
33 2.93e+04 2.77e+04 3.12e+02 2.00e-03 1.57e-03 4.54e+00
34 2.93e+04 2.77e+04 3.12e+02 1.84e-03 1.59e-03 5.13e+00
35 2.92e+04 2.77e+04 3.13e+02 1.69e-03 1.44e-03 5.13e+00
36 2.92e+04 2.77e+04 3.13e+02 1.56e-03 1.29e-03 5.13e+00
37 2.92e+04 2.77e+04 3.13e+02 1.44e-03 1.28e-03 5.65e+00
38 2.92e+04 2.77e+04 3.14e+02 1.32e-03 1.16e-03 5.65e+00
39 2.92e+04 2.77e+04 3.14e+02 1.21e-03 1.03e-03 5.65e+00
40 2.92e+04 2.77e+04 3.15e+02 1.12e-03 8.96e-04 5.65e+00
41 2.92e+04 2.76e+04 3.15e+02 1.03e-03 9.28e-04 6.32e+00
42 2.92e+04 2.76e+04 3.15e+02 9.44e-04 8.40e-04 6.32e+00
----------------------------------------------------------------
Display solve time and denoising performance.
print("SplineL1 solve time: %5.2f s" % b.timer.elapsed('solve'))
print("Noisy image PSNR: %5.2f dB" % metric.psnr(img, imgn))
print("Denoised image PSNR: %5.2f dB" % metric.psnr(img, imgr))
SplineL1 solve time: 0.52 s
Noisy image PSNR: 11.32 dB
Denoised image PSNR: 27.66 dB
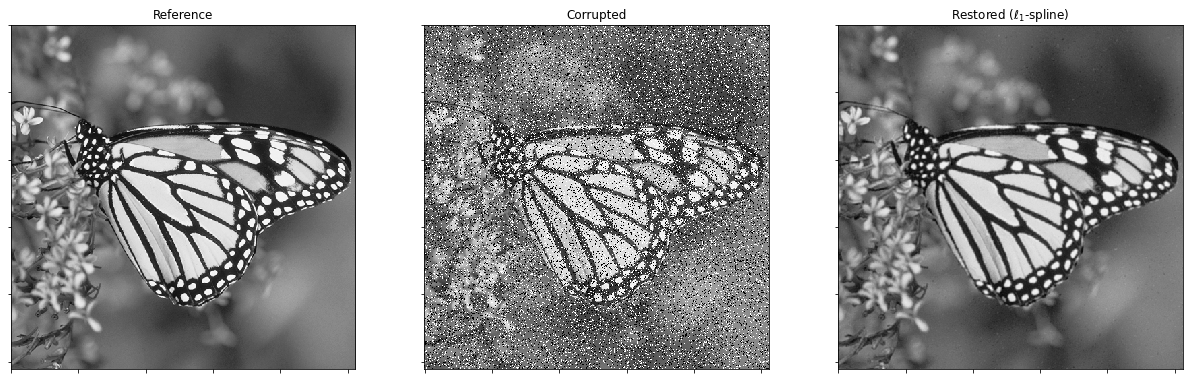
Display reference, corrupted, and denoised images.
fig = plot.figure(figsize=(21, 7))
plot.subplot(1, 3, 1)
plot.imview(img, title='Reference', fig=fig)
plot.subplot(1, 3, 2)
plot.imview(imgn, title='Corrupted', fig=fig)
plot.subplot(1, 3, 3)
plot.imview(imgr, title=r'Restored ($\ell_1$-spline)', fig=fig)
fig.show()
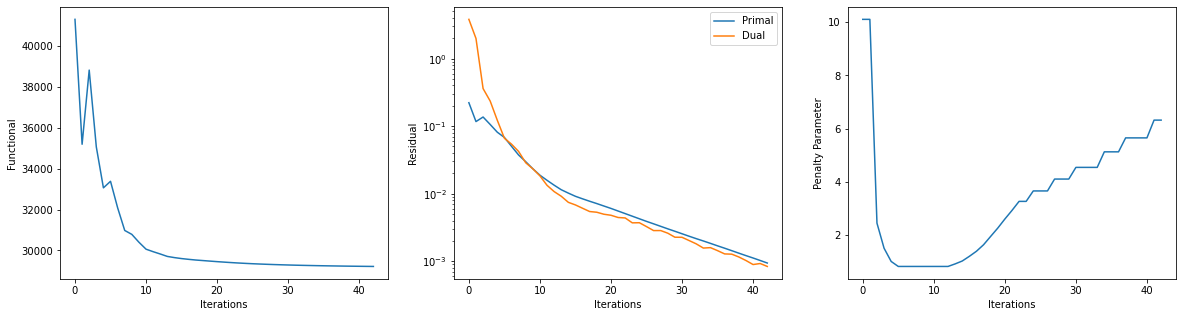
Get iterations statistics from solver object and plot functional value, ADMM primary and dual residuals, and automatically adjusted ADMM penalty parameter against the iteration number.
its = b.getitstat()
fig = plot.figure(figsize=(20, 5))
plot.subplot(1, 3, 1)
plot.plot(its.ObjFun, xlbl='Iterations', ylbl='Functional', fig=fig)
plot.subplot(1, 3, 2)
plot.plot(np.vstack((its.PrimalRsdl, its.DualRsdl)).T,
ptyp='semilogy', xlbl='Iterations', ylbl='Residual',
lgnd=['Primal', 'Dual'], fig=fig)
plot.subplot(1, 3, 3)
plot.plot(its.Rho, xlbl='Iterations', ylbl='Penalty Parameter', fig=fig)
fig.show()