Online Convolutional Dictionary Learning (CuPy Version)¶
This example demonstrates the use of
onlinecdl.OnlineConvBPDNDictLearn for learning a
convolutional dictionary from a set of training images. The dictionary
is learned using the online dictionary learning algorithm proposed in
[33]. This variant of the example uses the GPU
accelerated version of onlinecdl within the
sporco.cupy subpackage.
from __future__ import print_function
from builtins import input
import numpy as np
from sporco import util
from sporco import signal
from sporco import plot
plot.config_notebook_plotting()
from sporco.cupy import (cupy_enabled, np2cp, cp2np, select_device_by_load,
gpu_info)
from sporco.cupy.dictlrn import onlinecdl
Load training images.
exim = util.ExampleImages(scaled=True, zoom=0.25)
S1 = exim.image('barbara.png', idxexp=np.s_[10:522, 100:612])
S2 = exim.image('kodim23.png', idxexp=np.s_[:, 60:572])
S3 = exim.image('monarch.png', idxexp=np.s_[:, 160:672])
S4 = exim.image('sail.png', idxexp=np.s_[:, 210:722])
S5 = exim.image('tulips.png', idxexp=np.s_[:, 30:542])
S = np.stack((S1, S2, S3, S4, S5), axis=3)
Highpass filter training images.
npd = 16
fltlmbd = 5
sl, sh = signal.tikhonov_filter(S, fltlmbd, npd)
Construct initial dictionary.
np.random.seed(12345)
D0 = np.random.randn(8, 8, 3, 64)
Set regularization parameter and options for dictionary learning solver.
lmbda = 0.2
opt = onlinecdl.OnlineConvBPDNDictLearn.Options({
'Verbose': True, 'ZeroMean': False, 'eta_a': 10.0,
'eta_b': 20.0, 'DataType': np.float32,
'CBPDN': {'rho': 5.0, 'AutoRho': {'Enabled': True},
'RelaxParam': 1.8, 'RelStopTol': 1e-7, 'MaxMainIter': 50,
'FastSolve': False, 'DataType': np.float32}})
Create solver object and solve.
if not cupy_enabled():
print('CuPy/GPU device not available: running without GPU acceleration\n')
else:
id = select_device_by_load()
info = gpu_info()
if info:
print('Running on GPU %d (%s)\n' % (id, info[id].name))
d = onlinecdl.OnlineConvBPDNDictLearn(np2cp(D0), lmbda, opt)
iter = 50
d.display_start()
for it in range(iter):
img_index = np.random.randint(0, sh.shape[-1])
d.solve(np2cp(sh[..., [img_index]]))
d.display_end()
D1 = cp2np(d.getdict())
print("OnlineConvBPDNDictLearn solve time: %.2fs" % d.timer.elapsed('solve'))
Running on GPU 0 (NVIDIA GeForce RTX 2080 Ti)
Itn X r X s X ρ D cnstr D dlt D η
----------------------------------------------------------------
0 9.81e-04 1.58e-03 5.00e+00 8.03e+01 6.07e+00 5.00e-01
1 1.82e-03 1.59e-03 5.00e+00 7.30e+01 4.64e+00 4.76e-01
2 3.25e-03 2.01e-03 5.00e+00 2.38e+01 2.63e+00 4.55e-01
3 1.91e-03 1.91e-03 5.00e+00 4.86e+01 2.31e+00 4.35e-01
4 2.86e-03 1.80e-03 5.00e+00 2.00e+01 1.69e+00 4.17e-01
5 1.87e-03 1.53e-03 5.00e+00 3.53e+01 1.98e+00 4.00e-01
6 2.35e-03 3.19e-03 5.00e+00 3.60e+01 2.23e+00 3.85e-01
7 1.69e-03 1.87e-03 5.00e+00 4.22e+01 2.15e+00 3.70e-01
8 1.73e-03 1.51e-03 5.00e+00 3.19e+01 1.74e+00 3.57e-01
9 2.01e-03 2.87e-03 5.00e+00 3.23e+01 1.86e+00 3.45e-01
10 2.31e-03 1.91e-03 5.00e+00 1.58e+01 1.47e+00 3.33e-01
11 1.90e-03 2.79e-03 5.00e+00 2.98e+01 1.57e+00 3.23e-01
12 2.17e-03 1.87e-03 5.00e+00 2.49e+01 1.85e+00 3.12e-01
13 2.61e-03 2.11e-03 5.00e+00 1.38e+01 1.17e+00 3.03e-01
14 1.96e-03 2.23e-03 5.00e+00 3.45e+01 1.92e+00 2.94e-01
15 2.37e-03 1.98e-03 5.00e+00 1.33e+01 1.03e+00 2.86e-01
16 2.35e-03 2.16e-03 5.00e+00 2.16e+01 1.46e+00 2.78e-01
17 2.27e-03 3.43e-03 5.00e+00 2.64e+01 1.82e+00 2.70e-01
18 2.29e-03 2.04e-03 5.00e+00 1.25e+01 1.02e+00 2.63e-01
19 1.92e-03 2.32e-03 5.00e+00 2.98e+01 1.54e+00 2.56e-01
20 2.23e-03 2.11e-03 5.00e+00 1.95e+01 1.40e+00 2.50e-01
21 2.18e-03 1.90e-03 5.00e+00 2.13e+01 1.24e+00 2.44e-01
22 2.14e-03 3.30e-03 5.00e+00 2.33e+01 1.49e+00 2.38e-01
23 1.85e-03 2.24e-03 5.00e+00 2.75e+01 1.41e+00 2.33e-01
24 2.13e-03 1.98e-03 5.00e+00 1.78e+01 1.18e+00 2.27e-01
25 2.10e-03 1.89e-03 5.00e+00 1.99e+01 1.14e+00 2.22e-01
26 1.83e-03 2.28e-03 5.00e+00 2.58e+01 1.26e+00 2.17e-01
27 1.70e-03 2.18e-03 5.00e+00 2.48e+01 8.44e-01 2.13e-01
28 1.68e-03 2.22e-03 5.00e+00 2.44e+01 6.93e-01 2.08e-01
29 2.16e-03 1.96e-03 5.00e+00 1.59e+01 1.21e+00 2.04e-01
30 1.77e-03 2.36e-03 5.00e+00 2.40e+01 8.80e-01 2.00e-01
31 1.92e-03 1.67e-03 5.00e+00 1.75e+01 1.15e+00 1.96e-01
32 1.75e-03 1.60e-03 5.00e+00 1.76e+01 8.28e-01 1.92e-01
33 2.10e-03 1.94e-03 5.00e+00 1.48e+01 1.00e+00 1.89e-01
34 1.74e-03 2.23e-03 5.00e+00 2.26e+01 1.18e+00 1.85e-01
35 2.12e-03 2.02e-03 5.00e+00 1.43e+01 8.84e-01 1.82e-01
36 1.72e-03 2.25e-03 5.00e+00 2.16e+01 8.68e-01 1.79e-01
37 2.15e-03 2.10e-03 5.00e+00 1.39e+01 7.84e-01 1.75e-01
38 2.04e-03 1.82e-03 5.00e+00 1.57e+01 9.79e-01 1.72e-01
39 1.70e-03 2.23e-03 5.00e+00 2.08e+01 1.00e+00 1.69e-01
40 2.27e-03 3.35e-03 5.00e+00 1.62e+01 1.47e+00 1.67e-01
41 2.03e-03 3.22e-03 5.00e+00 1.58e+01 1.04e+00 1.64e-01
42 1.85e-03 3.02e-03 5.00e+00 1.58e+01 9.14e-01 1.61e-01
43 1.68e-03 2.84e-03 5.00e+00 1.58e+01 9.14e-01 1.59e-01
44 1.97e-03 1.74e-03 5.00e+00 1.38e+01 9.08e-01 1.56e-01
45 2.12e-03 1.96e-03 5.00e+00 1.21e+01 9.53e-01 1.54e-01
46 1.86e-03 3.08e-03 5.00e+00 1.57e+01 1.02e+00 1.52e-01
47 1.82e-03 2.28e-03 5.00e+00 1.83e+01 1.24e+00 1.49e-01
48 1.60e-03 2.72e-03 5.00e+00 1.52e+01 9.08e-01 1.47e-01
49 2.05e-03 1.96e-03 5.00e+00 1.14e+01 8.44e-01 1.45e-01
----------------------------------------------------------------
OnlineConvBPDNDictLearn solve time: 12.33s
Display initial and final dictionaries.
D1 = D1.squeeze()
fig = plot.figure(figsize=(14, 7))
plot.subplot(1, 2, 1)
plot.imview(util.tiledict(D0), title='D0', fig=fig)
plot.subplot(1, 2, 2)
plot.imview(util.tiledict(D1), title='D1', fig=fig)
fig.show()

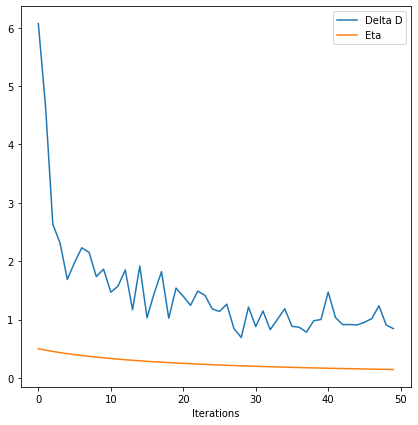
Get iterations statistics from solver object and plot functional value.
its = d.getitstat()
DeltaD = [float(x) for x in its.DeltaD]
fig = plot.figure(figsize=(7, 7))
plot.plot(np.vstack((DeltaD, its.Eta)).T, xlbl='Iterations',
lgnd=('Delta D', 'Eta'), fig=fig)
fig.show()