Lasso Optimisation¶
This example demonstrates the use of class bpdn.BPDNProjL1
to solve the least absolute shrinkage and selection operator (lasso)
problem [46]
where \(D\) is the dictionary, \(\mathbf{x}\) is the sparse representation, and \(\mathbf{s}\) is the signal to be represented. In this example the lasso problem is used to estimate the reference sparse representation that generated a signal from a noisy version of the signal.
from __future__ import print_function
from builtins import input
import numpy as np
from sporco.admm import bpdn
from sporco import plot
plot.config_notebook_plotting()
Configure problem size, sparsity, and noise level.
N = 512 # Signal size
M = 4*N # Dictionary size
L = 32 # Number of non-zero coefficients in generator
sigma = 0.5 # Noise level
Construct random dictionary, reference random sparse representation, and test signal consisting of the synthesis of the reference sparse representation with additive Gaussian noise.
# Construct random dictionary and random sparse coefficients
np.random.seed(12345)
D = np.random.randn(N, M)
x0 = np.zeros((M, 1))
si = np.random.permutation(list(range(0, M-1)))
x0[si[0:L]] = np.random.randn(L, 1)
# Construct reference and noisy signal
s0 = D.dot(x0)
s = s0 + sigma*np.random.randn(N,1)
Set bpdn.BPDNProjL1 solver class options. The value of
\(\gamma\) has been manually chosen for good performance.
gamma = 2.5e1
opt = bpdn.BPDNProjL1.Options({'Verbose': True, 'MaxMainIter': 500,
'RelStopTol': 1e-6, 'AutoRho': {'RsdlTarget': 1.0}})
Initialise and run BPDNProjL1 object
b = bpdn.BPDNProjL1(D, s, gamma, opt)
x = b.solve()
print("BPDNProjL1 solve time: %.2fs" % b.timer.elapsed('solve'))
Itn Fnc Cnstr r s ρ
------------------------------------------------------
0 1.65e+03 0.00e+00 6.90e-01 6.11e-01 1.00e+00
1 5.35e+02 0.00e+00 3.52e-01 5.17e-01 1.00e+00
2 6.26e+02 0.00e+00 2.15e-01 4.07e-01 1.00e+00
3 7.28e+02 0.00e+00 1.90e-01 1.57e-01 1.00e+00
4 4.10e+02 0.00e+00 1.79e-01 1.78e-01 1.00e+00
5 3.37e+02 0.00e+00 1.59e-01 1.95e-01 1.00e+00
6 4.04e+02 0.00e+00 1.71e-01 1.60e-01 1.00e+00
7 4.36e+02 0.00e+00 1.58e-01 1.30e-01 1.00e+00
8 3.84e+02 0.00e+00 1.46e-01 1.14e-01 1.00e+00
9 2.57e+02 0.00e+00 1.27e-01 1.20e-01 1.00e+00
10 2.89e+02 0.00e+00 1.14e-01 1.15e-01 1.00e+00
11 3.57e+02 0.00e+00 1.12e-01 7.90e-02 1.00e+00
12 2.53e+02 0.00e+00 1.09e-01 7.44e-02 1.00e+00
13 2.04e+02 0.00e+00 1.04e-01 8.63e-02 1.00e+00
14 2.57e+02 0.00e+00 1.07e-01 6.97e-02 1.00e+00
15 2.43e+02 0.00e+00 1.07e-01 5.62e-02 1.00e+00
16 2.10e+02 1.22e-15 1.01e-01 5.70e-02 1.00e+00
17 1.93e+02 0.00e+00 9.44e-02 5.36e-02 1.00e+00
18 1.85e+02 0.00e+00 8.87e-02 4.86e-02 1.00e+00
19 1.82e+02 4.84e-16 8.43e-02 4.29e-02 1.00e+00
20 1.44e+02 0.00e+00 7.71e-02 4.12e-02 1.40e+00
21 1.18e+02 0.00e+00 7.51e-02 4.95e-02 1.40e+00
22 1.41e+02 0.00e+00 7.57e-02 4.24e-02 1.40e+00
23 1.43e+02 0.00e+00 7.63e-02 3.03e-02 1.40e+00
24 1.20e+02 3.88e-18 7.33e-02 3.10e-02 1.40e+00
25 1.13e+02 1.02e-15 6.90e-02 3.13e-02 1.40e+00
26 1.13e+02 0.00e+00 6.61e-02 2.74e-02 1.40e+00
27 1.09e+02 0.00e+00 6.42e-02 2.25e-02 1.40e+00
28 1.06e+02 0.00e+00 6.29e-02 2.07e-02 1.40e+00
29 1.02e+02 0.00e+00 6.24e-02 2.01e-02 1.40e+00
30 9.23e+01 0.00e+00 5.83e-02 2.23e-02 2.47e+00
31 8.88e+01 0.00e+00 5.70e-02 2.37e-02 2.47e+00
32 8.93e+01 0.00e+00 5.62e-02 1.88e-02 2.47e+00
33 8.70e+01 4.92e-16 5.50e-02 1.61e-02 2.47e+00
34 8.61e+01 0.00e+00 5.40e-02 1.43e-02 2.47e+00
35 8.57e+01 0.00e+00 5.34e-02 1.27e-02 2.47e+00
36 8.47e+01 0.00e+00 5.28e-02 1.23e-02 2.47e+00
37 8.46e+01 8.18e-16 5.26e-02 1.12e-02 2.47e+00
38 8.43e+01 0.00e+00 5.25e-02 8.26e-03 2.47e+00
39 8.30e+01 0.00e+00 5.21e-02 7.74e-03 2.47e+00
40 8.06e+01 0.00e+00 5.07e-02 1.18e-02 6.41e+00
41 7.97e+01 0.00e+00 4.97e-02 1.65e-02 6.41e+00
42 8.13e+01 0.00e+00 4.92e-02 1.10e-02 6.41e+00
43 8.10e+01 0.00e+00 4.87e-02 6.68e-03 6.41e+00
44 7.99e+01 0.00e+00 4.82e-02 8.38e-03 6.41e+00
45 7.97e+01 1.65e-15 4.79e-02 8.45e-03 6.41e+00
46 7.99e+01 0.00e+00 4.76e-02 6.81e-03 6.41e+00
47 8.00e+01 7.90e-16 4.71e-02 5.42e-03 6.41e+00
48 7.97e+01 0.00e+00 4.66e-02 4.92e-03 6.41e+00
49 7.92e+01 3.67e-16 4.61e-02 5.14e-03 6.41e+00
50 7.87e+01 0.00e+00 4.50e-02 6.75e-03 1.92e+01
51 7.84e+01 3.55e-16 4.39e-02 8.73e-03 1.92e+01
52 7.84e+01 0.00e+00 4.29e-02 6.16e-03 1.92e+01
53 7.83e+01 0.00e+00 4.19e-02 4.65e-03 1.92e+01
54 7.81e+01 0.00e+00 4.09e-02 4.61e-03 1.92e+01
55 7.78e+01 0.00e+00 3.99e-02 3.95e-03 1.92e+01
56 7.76e+01 7.34e-16 3.90e-02 3.57e-03 1.92e+01
57 7.75e+01 0.00e+00 3.80e-02 3.33e-03 1.92e+01
58 7.75e+01 0.00e+00 3.72e-02 2.69e-03 1.92e+01
59 7.75e+01 1.12e-17 3.63e-02 2.17e-03 1.92e+01
60 7.73e+01 7.27e-16 3.42e-02 4.42e-03 7.86e+01
61 7.70e+01 0.00e+00 3.14e-02 7.09e-03 7.86e+01
62 7.67e+01 0.00e+00 2.89e-02 6.18e-03 7.86e+01
63 7.65e+01 1.12e-17 2.67e-02 4.48e-03 7.86e+01
64 7.63e+01 1.16e-17 2.47e-02 3.85e-03 7.86e+01
65 7.62e+01 0.00e+00 2.29e-02 3.44e-03 7.86e+01
66 7.61e+01 0.00e+00 2.12e-02 3.07e-03 7.86e+01
67 7.60e+01 7.36e-16 1.98e-02 2.86e-03 7.86e+01
68 7.59e+01 0.00e+00 1.85e-02 2.35e-03 7.86e+01
69 7.59e+01 0.00e+00 1.72e-02 1.92e-03 7.86e+01
70 7.58e+01 7.30e-16 1.51e-02 3.38e-03 2.36e+02
71 7.57e+01 7.27e-16 1.25e-02 5.35e-03 2.36e+02
72 7.57e+01 0.00e+00 1.05e-02 5.31e-03 2.36e+02
73 7.56e+01 0.00e+00 8.88e-03 4.67e-03 2.36e+02
74 7.55e+01 0.00e+00 7.53e-03 3.77e-03 2.36e+02
75 7.55e+01 7.27e-16 6.41e-03 2.82e-03 2.36e+02
76 7.55e+01 3.46e-16 5.47e-03 2.25e-03 2.36e+02
77 7.55e+01 1.26e-17 4.69e-03 2.17e-03 2.36e+02
78 7.55e+01 1.27e-17 4.03e-03 1.91e-03 2.36e+02
79 7.55e+01 1.30e-17 3.48e-03 1.65e-03 2.36e+02
80 7.55e+01 0.00e+00 2.90e-03 1.33e-03 3.42e+02
81 7.55e+01 0.00e+00 2.36e-03 1.39e-03 3.42e+02
82 7.55e+01 0.00e+00 1.93e-03 1.27e-03 3.42e+02
83 7.55e+01 0.00e+00 1.58e-03 9.73e-04 3.42e+02
84 7.55e+01 0.00e+00 1.30e-03 7.83e-04 3.42e+02
85 7.55e+01 0.00e+00 1.07e-03 6.55e-04 3.42e+02
86 7.55e+01 0.00e+00 8.80e-04 5.22e-04 3.42e+02
87 7.55e+01 0.00e+00 7.26e-04 4.97e-04 3.42e+02
88 7.55e+01 0.00e+00 6.00e-04 4.78e-04 3.42e+02
89 7.55e+01 0.00e+00 4.97e-04 3.75e-04 3.42e+02
90 7.55e+01 0.00e+00 4.05e-04 2.67e-04 3.94e+02
91 7.55e+01 0.00e+00 3.27e-04 2.07e-04 3.94e+02
92 7.55e+01 0.00e+00 2.65e-04 1.74e-04 3.94e+02
93 7.55e+01 3.38e-16 2.15e-04 1.69e-04 3.94e+02
94 7.55e+01 0.00e+00 1.75e-04 1.58e-04 3.94e+02
95 7.55e+01 0.00e+00 1.42e-04 1.27e-04 3.94e+02
96 7.55e+01 0.00e+00 1.15e-04 9.94e-05 3.94e+02
97 7.55e+01 0.00e+00 9.39e-05 7.30e-05 3.94e+02
98 7.55e+01 0.00e+00 7.64e-05 4.89e-05 3.94e+02
99 7.55e+01 0.00e+00 6.22e-05 3.34e-05 3.94e+02
100 7.55e+01 0.00e+00 4.89e-05 2.97e-05 5.37e+02
101 7.55e+01 0.00e+00 3.73e-05 3.33e-05 5.37e+02
102 7.55e+01 0.00e+00 2.85e-05 3.20e-05 5.37e+02
103 7.55e+01 0.00e+00 2.18e-05 2.66e-05 5.37e+02
104 7.55e+01 0.00e+00 1.67e-05 2.11e-05 5.37e+02
105 7.55e+01 0.00e+00 1.27e-05 1.63e-05 5.37e+02
106 7.55e+01 2.98e-17 9.72e-06 1.23e-05 5.37e+02
107 7.55e+01 0.00e+00 7.43e-06 9.54e-06 5.37e+02
108 7.55e+01 0.00e+00 5.68e-06 7.27e-06 5.37e+02
109 7.55e+01 0.00e+00 4.35e-06 5.37e-06 5.37e+02
110 7.55e+01 0.00e+00 3.39e-06 3.80e-06 4.84e+02
111 7.55e+01 1.35e-17 2.67e-06 2.56e-06 4.84e+02
112 7.55e+01 0.00e+00 2.10e-06 1.86e-06 4.84e+02
113 7.55e+01 6.97e-16 1.66e-06 1.54e-06 4.84e+02
114 7.55e+01 0.00e+00 1.31e-06 1.30e-06 4.84e+02
115 7.55e+01 0.00e+00 1.04e-06 1.05e-06 4.84e+02
116 7.55e+01 0.00e+00 8.22e-07 8.18e-07 4.84e+02
------------------------------------------------------
BPDNProjL1 solve time: 0.37s
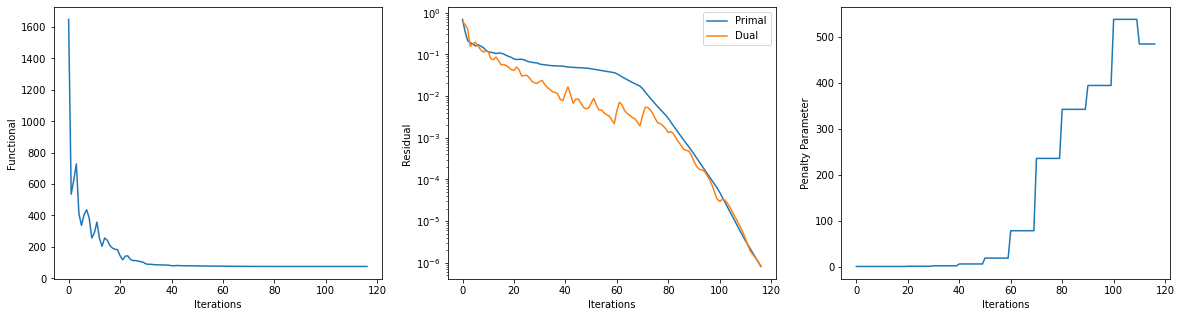
Plot comparison of reference and recovered representations.
plot.plot(np.hstack((x0, x)), title='Sparse representation',
lgnd=['Reference', 'Reconstructed'])
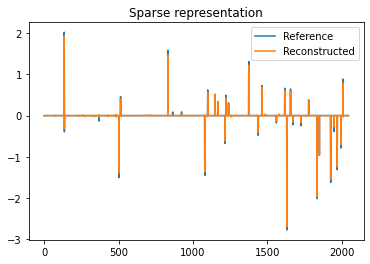
Plot functional value, residuals, and rho
its = b.getitstat()
fig = plot.figure(figsize=(20, 5))
plot.subplot(1, 3, 1)
plot.plot(its.ObjFun, xlbl='Iterations', ylbl='Functional', fig=fig)
plot.subplot(1, 3, 2)
plot.plot(np.vstack((its.PrimalRsdl, its.DualRsdl)).T,
ptyp='semilogy', xlbl='Iterations', ylbl='Residual',
lgnd=['Primal', 'Dual'], fig=fig)
plot.subplot(1, 3, 3)
plot.plot(its.Rho, xlbl='Iterations', ylbl='Penalty Parameter', fig=fig)
fig.show()